Reliability Generalization Workshop
Jiaxin Deng
2022/7/16
———-Table of Contents——————————————————————————————–
———- 1. Meta-analysis in R ————————————————————–
———- 2. Example: Deng et al. (2019) Reliability generalization of the
ICU———————–
———- Hands-on exercises: Practice with demo
data——————————————————-
———- 3. Summary——————————————————————————————
———- 4. Resources ——————————————————————————–
1. Meta-analysis in R
R programming is commonly used in the data analysis of meta-analysis and reliability generalization.
Several commonly used R packages in the meta-analysis include
metafor(Viechtbauer, 2010), metaSEM (Cheung,
2015), etc. For details, see Polanin et al. (2017). This review
summarizes 63 currently available packages for meta-analysis and
provides comparisons and suggestions for their use in terms of
functions.
Polanin, J. R., Hennessy, E. A., & Tanner-Smith, E. E. (2017). A Review of Meta-Analysis Packages in R. Journal of Educational and Behavioral Statistics, 42, 206–242.
One of the most widely used packages for conducting meta-analysis is
metafor, which was written and developed by Professor
Wolfgang Viechtbauer of Maastricht University in the Netherlands.
Compared with other packages, metafor covers the
statistical analysis process of meta-analysis quite comprehensively,
including calculating effect size, conducting moderator analysis,
analyzing publication bias, and using multi-level models to deal with
nested dependent variable effect size.
Many RG studies used themetaforpackage as a tool for
statistical analysis, such as:
[1] Blázquez-Rincón, D., Durán, J. I., & Botella, J. (2022). The fear of COVID-19 scale: a reliability generalization meta-analysis. Assessment, 29, 940–948.
[2] Rubio-Aparicio, M., Núñez-Núñez, R. M., Sánchez-Meca, J., López-Pina, J. A., Marín-Martínez, F., & López-López, J. A. (2020). The Padua Inventory–Washington State University Revision of obsessions and compulsions: A reliability generalization meta-analysis. Journal of Personality Assessment, 102, 113–123.
[3] Vicent, M., Rubio-Aparicio, M., Sánchez-Meca, J., & Gonzálvez, C. (2019). A reliability generalization meta-analysis of the child and adolescent perfectionism scale. Journal of Affective Disorders, 245, 533–544.
[4] Piqueras, J. A., Martín-Vivar, M., Sandin, B., San Luis, C., & Pineda, D. (2017). The Revised Child Anxiety and Depression Scale: A systematic review and reliability generalization meta-analysis. Journal of affective disorders, 218, 153–169.
[5] López-Pina, J. A., Sánchez-Meca, J., López-López, J. A., Marín-Martínez, F., Núñez-Núñez, R. M., Rosa-Alcázar, A. I., … & Ferrer-Requena, J. (2015). The Yale–Brown obsessive compulsive scale: A reliability generalization meta-analysis. Assessment, 22, 619–628.
Therefore, the following example studies will demonstrate how to
perform statistical analysis using the metafor package
(Viechtbauer, 2010).
##2. Example: Deng et al. (2019) Reliability generalization of the ICU
Brief introduction
The following is an RG example of the Inventory of Callous-Unemotional traits (Deng et al., 2019), specifically describe how to conduct an RG study, focusing on software operations for statistical analysis.
The 24-item scale contains three subscales, Callousness, Uncaring, and Unemotional, using Likert 4 scored. Here is a brief summary of the specific process:
Preparation
1. Literature search and screening
In this study, a total of 1,125 articles were downloaded from multiple databases using multiple keywords. After applying filtering criteria, 146 articles were ultimately retained.
2. Data extraction and encoding
- Effect size: the total score and its subscale Cronbach’s alpha
coefficient
- The moderators are included as follows:
- SD of age
- Mean age
- % of males in sample
- sample size
- SD of total scores
- Mean of total scores
- administration format
- age group
- sample type
- language version
- country
- item number version
- Data analysis In this section, the total score α coefficient of the
scale (24 items) and the moderators of 53 studies in this study were
selected as demo data.
- effect size: the alpha coefficient of the total score of the
scale
- Continuous variables: sample size, mean age and standard deviation,
gender percentage, mean and standard deviation of the total score
- Categorical variables: age type, sample type, language, adminstration ratings
Examples of specific encoding rules are as follows:
criteria %>% knitr::kable()| variable | c1 | c2 | c3 | c4 |
|---|---|---|---|---|
| agetype | Infants and young children | Children | Adolescents | Adults |
| sampletype | community | offender | NA | NA |
| language | english | non-english | NA | NA |
| ratingformat | self-report | parent-report | teacher-report | NA |
Next, I will demonstrate how to conduct the analysis using demo data.
2.1.1 Installation and load packages
First, install and run the package. The code is displayed as follows:
library(readxl)
library(openxlsx)
options(tidyverse.quiet = TRUE)
library (tidyverse)
library(metafor)2.1.2 Data reading and import
To use the example shown, you first need to import the data. Since
the data file is in Excel format, you can use the readxl
package to read and import the data. Use this code with the appropriate
file path to import the data.
data<-read_excel("example_data.xlsx") #demo data in the current working directory
head(data,10)#10 rows## # A tibble: 10 × 13
## `study ID` agetype sampletype language ratingformat ageM ageSD gender size
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 1 3 1 1 1 15.0 1.3 0 58
## 2 2 3 2 2 1 16.7 1.34 0.56 352
## 3 3 3 1 1 1 15.9 1.53 1 150
## 4 4 3 1 1 1 15.2 1.4 0.6 150
## 5 5 4 2 1 1 19.9 3.48 0.3 602
## 6 6 3 2 1 1 16.9 0.8 0.48 675
## 7 7 3 2 2 1 16 0.89 0.503 2306
## 8 8 2 2 2 1 10 1.19 1 46
## 9 9 4 2 1 1 21.3 4.65 0.224 687
## 10 10 3 1 1 1 15.3 1.34 0.716 134
## # ℹ 4 more variables: totalSD <dbl>, totalM <dbl>, alpha_total <dbl>, mi <dbl>#data consists of 3 parts:
#(1) Effect size: alpha
#(2) Continuous regulation variables
#(3) Categorical moderators
#read_excel("path/to/data_file.xlsx") #specific path2.2 Heterogeneity testing
To examine heterogeneity in the effect size, the variability of the α
coefficients was mainly tested using the rma()
function.
Before testing for heterogeneity, the effect size needs to be
calculated, which is done mainly by the escalc()
function.
The escalc() function include the following
parameters:
(1) measure is used to convert Cronbach’s α coefficient or use the
original value;
(2) ai is the observed Cronbach’s α coefficient;
(3) ni is the sample size and mi is the number of items;
(4) dat is the dataset.
For example, to use the form without transformation, set measure to “ARAW” with the following code:
#raw alpha
total_es_raw<-escalc(measure = "ARAW", ai=alpha_total, ni=size, mi=mi, dat=data)
total_es_raw[1:10,]#yi--effect size,vi--sampling variance; the first 10 rows##
## study.ID agetype sampletype language ratingformat ageM ageSD gender size
## 1 1 3 1 1 1 14.98 1.30000 0.000 58
## 2 2 3 2 2 1 16.67 1.34000 0.560 352
## 3 3 3 1 1 1 15.89 1.53000 1.000 150
## 4 4 3 1 1 1 15.20 1.40000 0.600 150
## 5 5 4 2 1 1 19.90 3.48000 0.300 602
## 6 6 3 2 1 1 16.90 0.80000 0.480 675
## 7 7 3 2 2 1 16.00 0.89000 0.503 2306
## 8 8 2 2 2 1 10.00 1.18875 1.000 46
## 9 9 4 2 1 1 21.30 4.65000 0.224 687
## 10 10 3 1 1 1 15.34 1.34000 0.716 134
## totalSD totalM alpha_total mi yi vi
## 1 9.17 23.50 0.79 24 0.7900 0.0016
## 2 9.17 24.05 0.83 24 0.8300 0.0002
## 3 7.41 28.70 0.64 24 0.6400 0.0018
## 4 6.04 46.50 0.84 24 0.8400 0.0004
## 5 7.53 41.79 0.80 24 0.8000 0.0001
## 6 7.85 21.62 0.79 24 0.7900 0.0001
## 7 8.72 23.65 0.80 24 0.8000 0.0000
## 8 7.23 20.30 0.73 24 0.7300 0.0035
## 9 6.75 37.44 0.81 24 0.8100 0.0001
## 10 10.11 41.64 0.85 24 0.8500 0.0004If use the Bonett (2002) formula for conversion, set measure to “ABT” with the following code:
#use Bonett's (2002) formula to convert and calculate the weighted average alpha coefficient
total_es <- escalc("ABT",-ln(1-ai), ai=alpha_total, ni=size, mi=mi, dat=data)
total_es[1:10,] #yi--effect size, vi--sampling variance; Look at the first 10 rows##
## study.ID agetype sampletype language ratingformat ageM ageSD gender size
## 1 1 3 1 1 1 14.98 1.30000 0.000 58
## 2 2 3 2 2 1 16.67 1.34000 0.560 352
## 3 3 3 1 1 1 15.89 1.53000 1.000 150
## 4 4 3 1 1 1 15.20 1.40000 0.600 150
## 5 5 4 2 1 1 19.90 3.48000 0.300 602
## 6 6 3 2 1 1 16.90 0.80000 0.480 675
## 7 7 3 2 2 1 16.00 0.89000 0.503 2306
## 8 8 2 2 2 1 10.00 1.18875 1.000 46
## 9 9 4 2 1 1 21.30 4.65000 0.224 687
## 10 10 3 1 1 1 15.34 1.34000 0.716 134
## totalSD totalM alpha_total mi yi vi
## 1 9.17 23.50 0.79 24 1.5606 0.0373
## 2 9.17 24.05 0.83 24 1.7720 0.0060
## 3 7.41 28.70 0.64 24 1.0217 0.0141
## 4 6.04 46.50 0.84 24 1.8326 0.0141
## 5 7.53 41.79 0.80 24 1.6094 0.0035
## 6 7.85 21.62 0.79 24 1.5606 0.0031
## 7 8.72 23.65 0.80 24 1.6094 0.0009
## 8 7.23 20.30 0.73 24 1.3093 0.0474
## 9 6.75 37.44 0.81 24 1.6607 0.0030
## 10 10.11 41.64 0.85 24 1.8971 0.0158After calculating the effect size, the rma() function is
used for heterogeneity testing.
#heterogeneity
het1<-rma(total_es, yi, vi)
het1##
## Random-Effects Model (k = 53; tau^2 estimator: REML)
##
## tau^2 (estimated amount of total heterogeneity): 0.0782 (SE = 0.0178)
## tau (square root of estimated tau^2 value): 0.2797
## I^2 (total heterogeneity / total variability): 92.31%
## H^2 (total variability / sampling variability): 13.01
##
## Test for Heterogeneity:
## Q(df = 52) = 576.2518, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## 1.6587 0.0415 40.0034 <.0001 1.5775 1.7400 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1pred1=predict(het1, transf=transf.iabt)#back-transformation to alpha
pred1##
## pred ci.lb ci.ub pi.lb pi.ub
## 0.8096 0.7935 0.8245 0.6686 0.8906In addition, you can calculate the effect size and heterogeneity
tests directly with rma() in one step, as shown below:
het2<-rma(measure="ABT", ai=alpha_total, ni=size, mi=mi, dat=data)#default REML
het2##
## Random-Effects Model (k = 53; tau^2 estimator: REML)
##
## tau^2 (estimated amount of total heterogeneity): 0.0782 (SE = 0.0178)
## tau (square root of estimated tau^2 value): 0.2797
## I^2 (total heterogeneity / total variability): 92.31%
## H^2 (total variability / sampling variability): 13.01
##
## Test for Heterogeneity:
## Q(df = 52) = 576.2518, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## 1.6587 0.0415 40.0034 <.0001 1.5775 1.7400 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1pred2=predict(het2, transf=transf.iabt)##back-transformation to alpha
pred2##
## pred ci.lb ci.ub pi.lb pi.ub
## 0.8096 0.7935 0.8245 0.6686 0.8906The results from comparing HET1 and HET2 are the same, indicating
that either of them can be used.
Furthermore, you can choose different estimation methods by setting the
method parameter. The Restricted Maximum Likelihood method
(REML) is generally used by default. If you want to use other estimation
methods, you can set method="ML" to use maximum likelihood
estimation.
#method=ML
het3<-rma(total_es, yi, vi, method="ML")
het3##
## Random-Effects Model (k = 53; tau^2 estimator: ML)
##
## tau^2 (estimated amount of total heterogeneity): 0.0765 (SE = 0.0172)
## tau (square root of estimated tau^2 value): 0.2767
## I^2 (total heterogeneity / total variability): 92.16%
## H^2 (total variability / sampling variability): 12.75
##
## Test for Heterogeneity:
## Q(df = 52) = 576.2518, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## 1.6588 0.0411 40.3876 <.0001 1.5783 1.7393 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1pred3=predict(het3, transf=transf.iabt)#back-transformation to alpha
pred3##
## pred ci.lb ci.ub pi.lb pi.ub
## 0.8096 0.7937 0.8244 0.6706 0.8900Interpretation of the results:
The figure above shows the results of estimation using a random-effects model, with 53 effect sizes and maximum likelihood estimation.
Four indicators are provided for evaluating the heterogeneity: τ, τ2, H2, and I2. Among them, I2 is about 92%, indicating a high level of heterogeneity according to the criteria.
The Q value is 576.2518 with p<.0001, indicating that the heterogeneity test was significant.
Based on the results of the different estimation methods, heterogeneity exists. Therefore, it is necessary to further explore the factors contributing to the heterogeneity of these α coefficients.
In addition to directly extracting the results, you can also use code to organize the results in R, which is more convenient and fast.
—- this part is mainly based on R if and loop code, and does not involve reliability generalization analysis, so it will not be further expanded here. —-
The following table shows the results of the heterogeneity analysis.
het3_res %>% knitr::kable()| k | mean_alpha | CI.LB | CI.UB | Tau2 | Q | I2_precent |
|---|---|---|---|---|---|---|
| 53 | 0.81 | 0.79 | 0.82 | 0.077 | 576.252*** | 92.16 |
2.3 Forest plot
Use the forest.rma() function to build a forest plot to
visualize the distribution of effect size.
forest.rma(het3)#transformed alpha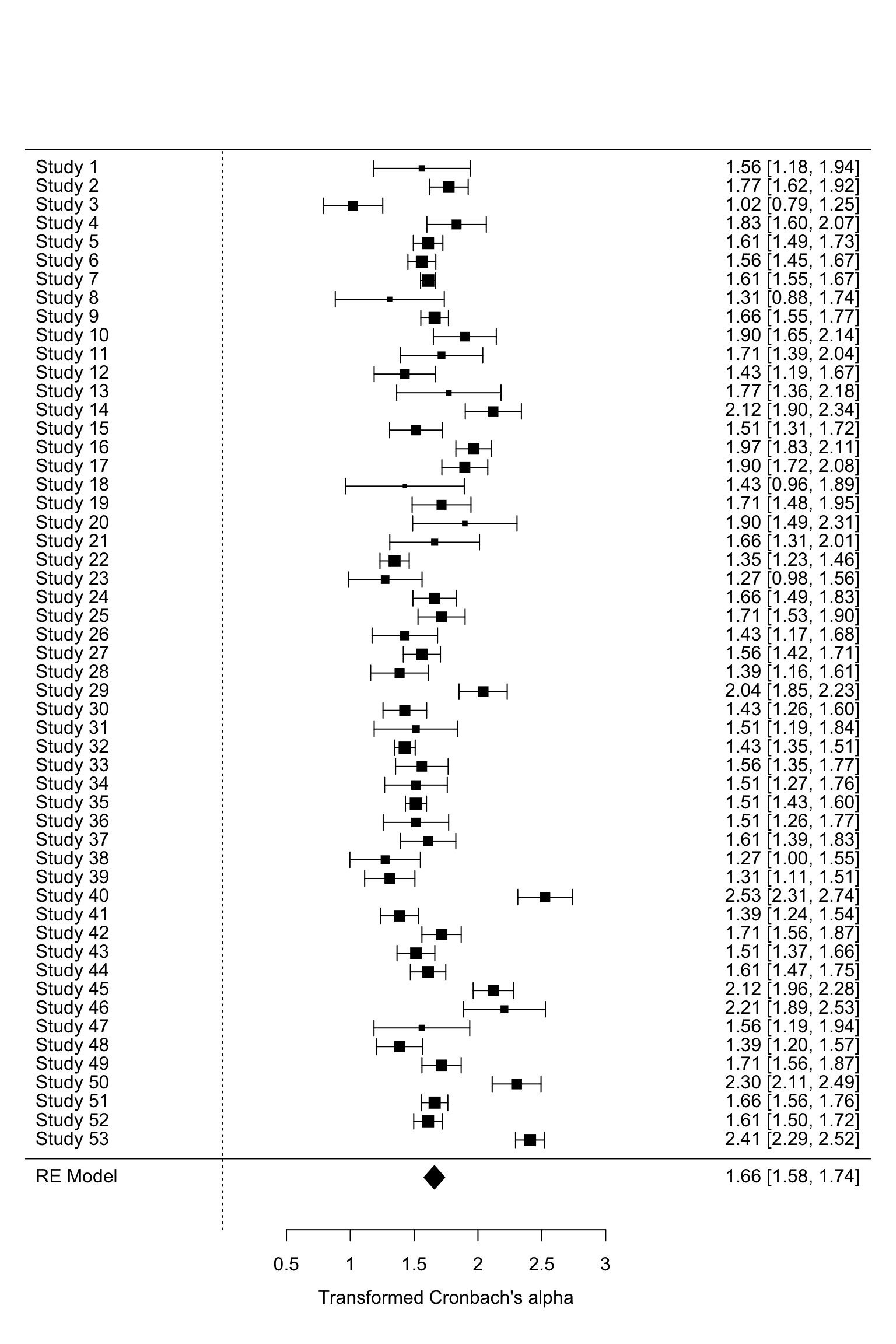
Interpretation of the results: The figure displays the name of each
study in the first column, the distribution of effect size in the
middle, and the effect size corresponding to each study and their
confidence interval on the right.
You can also adjust the parameters as needed. Here are some
options:
(1) Set annotate=TRUE to add labels to the figure. This is
generally the default setting.
(2) Use transf to convert the effect size.
(3) Use showweights to set the weights for presenting the
impact of each studies on the overall effect size.
(4) Use header to determine whether to include a header in
the figure.
The specific code is as follows:
forest.rma(het3,annotate=TRUE,transf=transf.iabt,header = TRUE,showweights=TRUE)#backtransformed alpha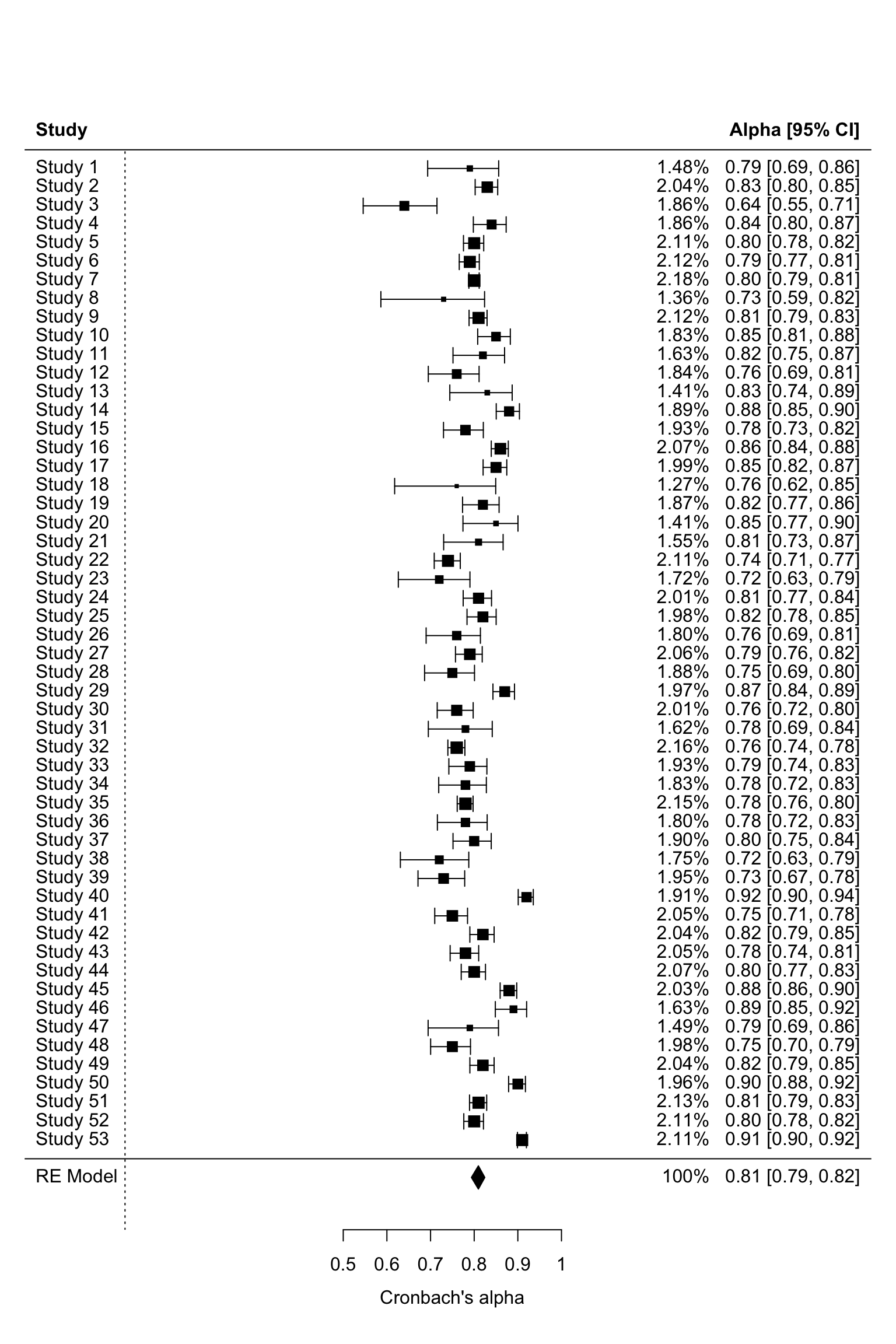
Interpretation of the results:
(1) A mean effect of 0.81 was estimated using a random-effects
model.
(2) The analysis yielded a mean α coefficient of 0.81, indicating good
internal consistency.
To save the result graph as a pdf, use the following code:
pdf("forestplot.pdf",width=10, height=20)
forest.rma(het3,annotate=TRUE,transf=transf.iabt,header = TRUE,showweights=TRUE)#backtransformed alpha
dev.off()## quartz_off_screen
## 22.4 Moderator analysis
Moderator analysis is mainly done by setting the mods
parameter in rma() in order to analyze the effect of the
included moderator on heterogeneity results.
The analysis parameter setting is typically used:
rma (total_es, yi, vi, mods = ~ moderator).
2.4.1 Example of a continuous variable
Using the standard deviation of the total score of the scale as an example, the code to include a single moderator for analysis is as follows:
res_tot_totalSD<-rma(total_es, yi, vi, mods=~totalSD,method="ML")
res_tot_totalSD##
## Mixed-Effects Model (k = 53; tau^2 estimator: ML)
##
## tau^2 (estimated amount of residual heterogeneity): 0.0521 (SE = 0.0124)
## tau (square root of estimated tau^2 value): 0.2282
## I^2 (residual heterogeneity / unaccounted variability): 88.81%
## H^2 (unaccounted variability / sampling variability): 8.94
## R^2 (amount of heterogeneity accounted for): 31.99%
##
## Test for Residual Heterogeneity:
## QE(df = 51) = 405.6720, p-val < .0001
##
## Test of Moderators (coefficient 2):
## QM(df = 1) = 20.9010, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## intrcpt 0.7581 0.2003 3.7851 0.0002 0.3655 1.1506 ***
## totalSD 0.1051 0.0230 4.5718 <.0001 0.0600 0.1502 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1res_tot_totalSD<-rma(measure="ABT", ai=alpha_total, ni=size, mi=mi, mods=~totalSD,dat= data,method="ML") #same results, the difference is that the variables in the dataset are used directly
res_tot_totalSD##
## Mixed-Effects Model (k = 53; tau^2 estimator: ML)
##
## tau^2 (estimated amount of residual heterogeneity): 0.0521 (SE = 0.0124)
## tau (square root of estimated tau^2 value): 0.2282
## I^2 (residual heterogeneity / unaccounted variability): 88.81%
## H^2 (unaccounted variability / sampling variability): 8.94
## R^2 (amount of heterogeneity accounted for): 31.99%
##
## Test for Residual Heterogeneity:
## QE(df = 51) = 405.6720, p-val < .0001
##
## Test of Moderators (coefficient 2):
## QM(df = 1) = 20.9010, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## intrcpt 0.7581 0.2003 3.7851 0.0002 0.3655 1.1506 ***
## totalSD 0.1051 0.0230 4.5718 <.0001 0.0600 0.1502 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Interpretation of the results:
(1) The moderator analysis used the the maximum likelihood estimation
based on the mixed-effects model, as shown in the first row.
(2) The effect of the moderators are also reported, with
p<.0001, indicating that the standard deviation of the total
score of the scale has a moderating effect on the effect size.
In addition to directly extracting the results after analyzing each variable, you can also use code in R and organize the results, which is convenient and fast.
—– This section mainly involves R if and loop code and does not involve reliability generalization analysis. Therefore, it will not be further expanded here. —-
The following table shows the results of the moderator analysis of continuous variables included.
reg_res %>% knitr::kable()| variable | k | b | t | sig.t | R2_percentage | QE |
|---|---|---|---|---|---|---|
| ageM | 53 | -0.010 | -1.160 | 0.246 | 3.57 | 518.487 *** |
| ageSD | 53 | -0.018 | -0.591 | 0.555 | 0.66 | 573.47 *** |
| gender | 53 | 0.127 | 0.934 | 0.350 | 2.10 | 563.457 *** |
| size | 53 | 0.000 | -0.310 | 0.757 | 0.34 | 563.269 *** |
| totalSD | 53 | 0.105 | 4.572 | 0.000 | 31.99 | 405.672 *** |
| totalM | 53 | 0.005 | 1.053 | 0.292 | 1.63 | 576.245 *** |
#b=beta
#t=significance test of moderator regression coefficient--zval
#sig.t=p-value
#R2% explain2.4.2 Examples of categorical variables
To present an analysis of categorical variables in moderator analysis using the example of administration ratings, the following code is shown as follows:
(1) Subgroup Analysis
sub_1=rma(total_es, yi, vi, subset = (total_es$ratingformat == 1))
predict(sub_1, transf=transf.iabt) #backtransformed alpha##
## pred ci.lb ci.ub pi.lb pi.ub
## 0.8047 0.7878 0.8202 0.6725 0.8835sub_2=rma (total_es, yi, vi, subset = (total_es$ratingformat == 2))
predict(sub_2, transf=transf.iabt)#backtransformed alpha##
## pred ci.lb ci.ub pi.lb pi.ub
## 0.8203 0.7711 0.8588 0.6757 0.9004sub_3=rma (total_es, yi, vi, subset = (total_es$ratingformat == 3))
predict(sub_3, transf=transf.iabt) #backtransformed alpha##
## pred ci.lb ci.ub pi.lb pi.ub
## 0.8717 0.7335 0.9383 0.5565 0.9629The table below shows the results of the subgroup analysis.
mod_res %>% knitr::kable()| group | k | alpha | ci_95 |
|---|---|---|---|
| Infants and young children | 1 | 0.91 | [ 0.9 , 0.92 ] |
| Children | 9 | 0.80 | [ 0.74 , 0.85 ] |
| Adolescents | 34 | 0.81 | [ 0.79 , 0.83 ] |
| Adults | 9 | 0.80 | [ 0.79 , 0.81 ] |
| community | 18 | 0.82 | [ 0.79 , 0.85 ] |
| offender | 35 | 0.80 | [ 0.79 , 0.82 ] |
| english | 34 | 0.81 | [ 0.79 , 0.82 ] |
| non-english | 19 | 0.82 | [ 0.79 , 0.84 ] |
| self-report | 45 | 0.80 | [ 0.79 , 0.82 ] |
| parent-report | 6 | 0.82 | [ 0.77 , 0.86 ] |
| teacher-report | 2 | 0.87 | [ 0.73 , 0.94 ] |
(2) Meta-Anova
res_tot_adf<-rma(total_es, yi, vi,mods=~ratingformat,method="ML")
res_tot_adf##
## Mixed-Effects Model (k = 53; tau^2 estimator: ML)
##
## tau^2 (estimated amount of residual heterogeneity): 0.0692 (SE = 0.0158)
## tau (square root of estimated tau^2 value): 0.2630
## I^2 (residual heterogeneity / unaccounted variability): 91.30%
## H^2 (unaccounted variability / sampling variability): 11.49
## R^2 (amount of heterogeneity accounted for): 9.64%
##
## Test for Residual Heterogeneity:
## QE(df = 51) = 434.7357, p-val < .0001
##
## Test of Moderators (coefficient 2):
## QM(df = 1) = 4.2441, p-val = 0.0394
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## intrcpt 1.4559 0.1061 13.7171 <.0001 1.2479 1.6639 ***
## ratingformat 0.1718 0.0834 2.0601 0.0394 0.0084 0.3352 *
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The results of the effect of the moderators were reported,p<.05, indicating that the effect was on the adminstration ratings.
The following table is the result of the moderator analysis of categorical variables.
anv_res %>% knitr::kable()| variable | k | R2_percentage | QB | sig |
|---|---|---|---|---|
| agetype | 53 | 6.13 | 2.480 | 0.115 |
| sampletype | 53 | 2.05 | 1.026 | 0.311 |
| language | 53 | 1.02 | 0.506 | 0.477 |
| ratingformat | 53 | 9.64 | 4.244 | 0.039 |
2.4.3 Examples of exploratory models
Select the above variables with moderating effect or high explanatory percentage into the model for analysis, and the specific code is as follows:
#full model
res_multi<-rma(total_es, yi, vi, mods=~ageM+totalM+totalSD+ratingformat,method="ML")
res_multi#R2=36.79%##
## Mixed-Effects Model (k = 53; tau^2 estimator: ML)
##
## tau^2 (estimated amount of residual heterogeneity): 0.0484 (SE = 0.0116)
## tau (square root of estimated tau^2 value): 0.2200
## I^2 (residual heterogeneity / unaccounted variability): 87.70%
## H^2 (unaccounted variability / sampling variability): 8.13
## R^2 (amount of heterogeneity accounted for): 36.79%
##
## Test for Residual Heterogeneity:
## QE(df = 48) = 333.9638, p-val < .0001
##
## Test of Moderators (coefficients 2:5):
## QM(df = 4) = 25.0511, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## intrcpt 0.6577 0.2803 2.3468 0.0189 0.1084 1.2070 *
## ageM -0.0024 0.0087 -0.2768 0.7819 -0.0194 0.0146
## totalM 0.0040 0.0041 0.9920 0.3212 -0.0039 0.0120
## totalSD 0.0944 0.0233 4.0558 <.0001 0.0488 0.1400 ***
## ratingformat 0.0996 0.0836 1.1911 0.2336 -0.0643 0.2634
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 12.5 Publication bias
2.5.1 Funnel plot
Funnel plot is a common analytical technique for sensitivity
analysis, which can visually detect whether the current study is
biased.
The specific code is as follows:
funplot1=funnel(het3,atransf=transf.iabt) #funnel plot
funplot2=funnel(het3,atransf=transf.iabt,label = TRUE)#studyID tag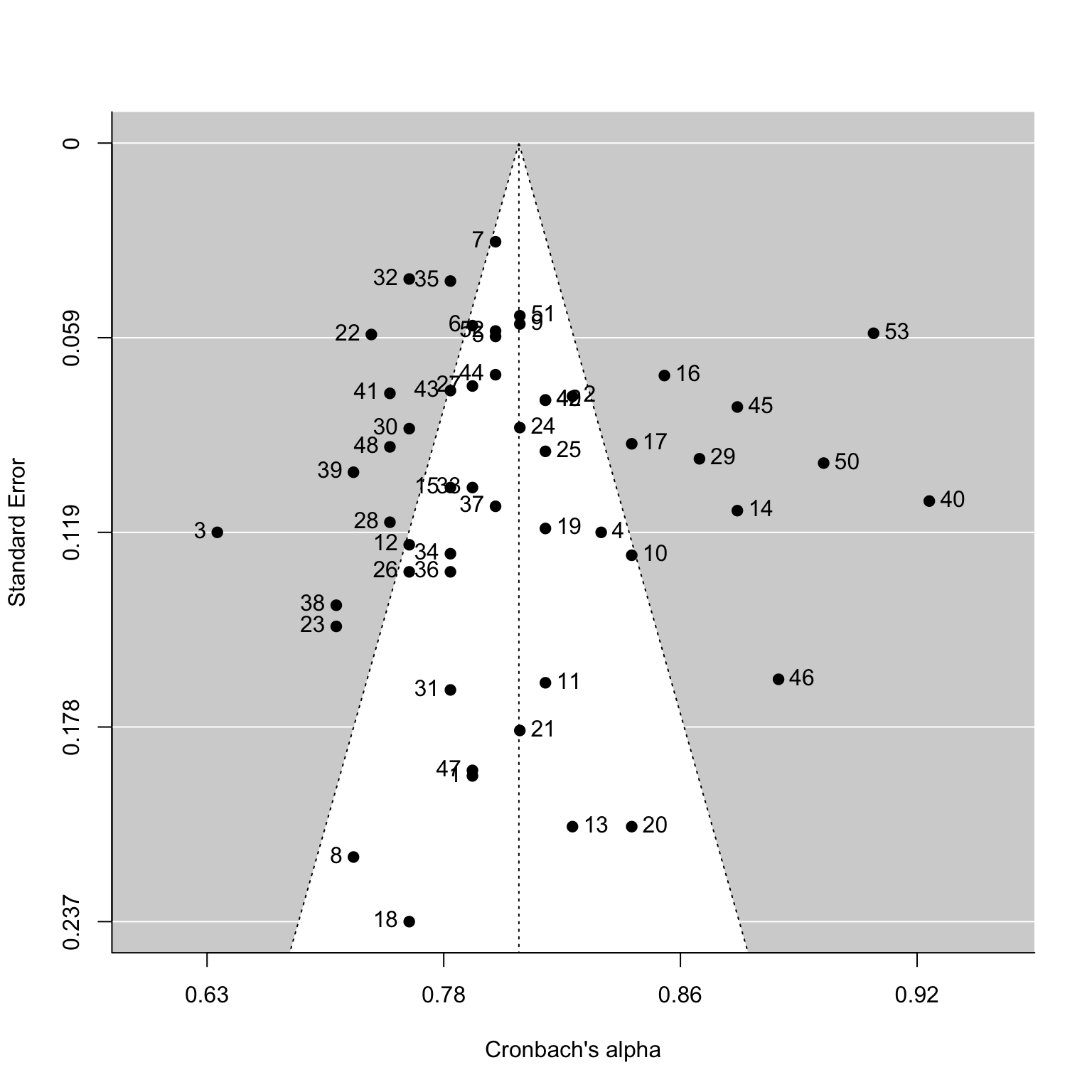
Interpretation of the results:
As can be seen from the figure, scatter points are mainly distributed at
the top of the funnel and concentrated in the middle, indicating no or
low probability of publication bias.
In addition, the Trim-and-fill method was used to analyze for publication bias as follows:
tf=trimfill(het3,estimator = "R0") #Trim-and-fill
tf##
## Estimated number of missing studies on the right side: 0 (SE = 1.4142)
## Test of H0: no missing studies on the right side: p-val = 0.5000
##
## Random-Effects Model (k = 53; tau^2 estimator: ML)
##
## tau^2 (estimated amount of total heterogeneity): 0.0765 (SE = 0.0172)
## tau (square root of estimated tau^2 value): 0.2767
## I^2 (total heterogeneity / total variability): 92.16%
## H^2 (total variability / sampling variability): 12.75
##
## Test for Heterogeneity:
## Q(df = 52) = 576.2518, p-val < .0001
##
## Model Results:
##
## estimate se zval pval ci.lb ci.ub
## 1.6588 0.0411 40.3876 <.0001 1.5783 1.7393 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Interpretation of the results:
Estimates using the Trim-and-fill method found that the number of
missing studies on the right side of the estimate was 0, indicating no
bias.
In addition, the correlation between effect size and sampling variance can be further analyzed. If the correlation is high, it indicates that the funnel graph is asymmetric, that is, there is bias.
ranktest (total_es$yi, total_es$vi,exact=FALSE) #correlation coefficient 0.05 - Low correlation - funnel plot is symmetric - no or low risk of bias. ##
## Rank Correlation Test for Funnel Plot Asymmetry
##
## Kendall's tau = 0.0494, p = 0.60192.5.2 Fail-safe N
Use the fsn() function to calculate the Fail-safe N with
the following code:
fail_safe=fsn(yi, vi, data=total_es,type="Rosenthal")
fail_safe##
## Fail-safe N Calculation Using the Rosenthal Approach
##
## Observed Significance Level: <.0001
## Target Significance Level: 0.05
##
## Fail-safe N: 3599835*nrow(data)+10# was compared to the calculated results of 5*k+10 (k is the number of included analyses).## [1] 275Interpretation of the results: (1) Line 1 indicates that the
Fail-safe N was calculated using the “Rosenthal” method.
(2) The Fail-safe N is compared to the calculated result of 5*k + 10
(where k is the number of included analyses). If the Fail-safe N is less
than the calculated value, then there is a risk of publication
bias.
(3) The results show the Fail-safe N of 359983, which is much higher
than the number included in the analysis, indicating no publication
bias.
In general, Fail-safe N are generally collated with heterogeneity results, as follows:
het3_res %>% knitr::kable()| k | mean_alpha | CI.LB | CI.UB | Tau2 | Q | I2_precent | FSN |
|---|---|---|---|---|---|---|---|
| 53 | 0.81 | 0.79 | 0.82 | 0.077 | 576.252*** | 92.16 | 359983*** |
2.5.3 Calculate the Egger’s regression test
Use the regtest() function for the Egger’s regression
test as follows:
regtest(het3, model="lm")### classical Egger test##
## Regression Test for Funnel Plot Asymmetry
##
## Model: weighted regression with multiplicative dispersion
## Predictor: standard error
##
## Test for Funnel Plot Asymmetry: t = 0.5984, df = 51, p = 0.5522
## Limit Estimate (as sei -> 0): b = 1.6015 (CI: 1.4359, 1.7672)Interpretation of the results: From the results, the Egger regression coefficient intercept was not significant, indicating that there was no bias or the possibility of bias was low.
2.5.4 Summary
In summary, the results of multiple analyses, including funnel plot, Trim-and-fill method, Rosenthal Fail-safe N, and Egger’s regression test, indicate a low risk of bias or the absence of publication bias in this study.
bias %>% knitr::kable()| method | results |
|---|---|
| funnelplot | symmetrical |
| fsn | Fail-safe N: 359983 > 5*53+10=275 |
| egger | t = 0.5984, df = 51, p = 0.5522 |
2.6 Export the results
After all the analysis is completed, use the write()
function to export the results for use in a paper or analysis
report.
#write.xlsx (het3_res, file = "heterogeneity test results.xlsx")
#write.xlsx (reg_res, file = "continuous moderator results.xlsx")
#write.xlsx (anv_res, file = "categorical moderator results.xlsx")Practice
Try using the built-in data dat.bonett2010 to complete a
full analysis process. The code for importing the data is provided
below:
dat <- dat.bonett2010
#description: Results from 9 studies on the reliability of the Center for Epidemiologic Studies Depression (CES-D) Scale administered to children providing care to an elderly parent.3. Summary
First, the statistical analysis process of reliability generalization
is described usingmetaforwith examples, including effect
size calculation, heterogeneity testing, moderation analysis, and
publication bias.
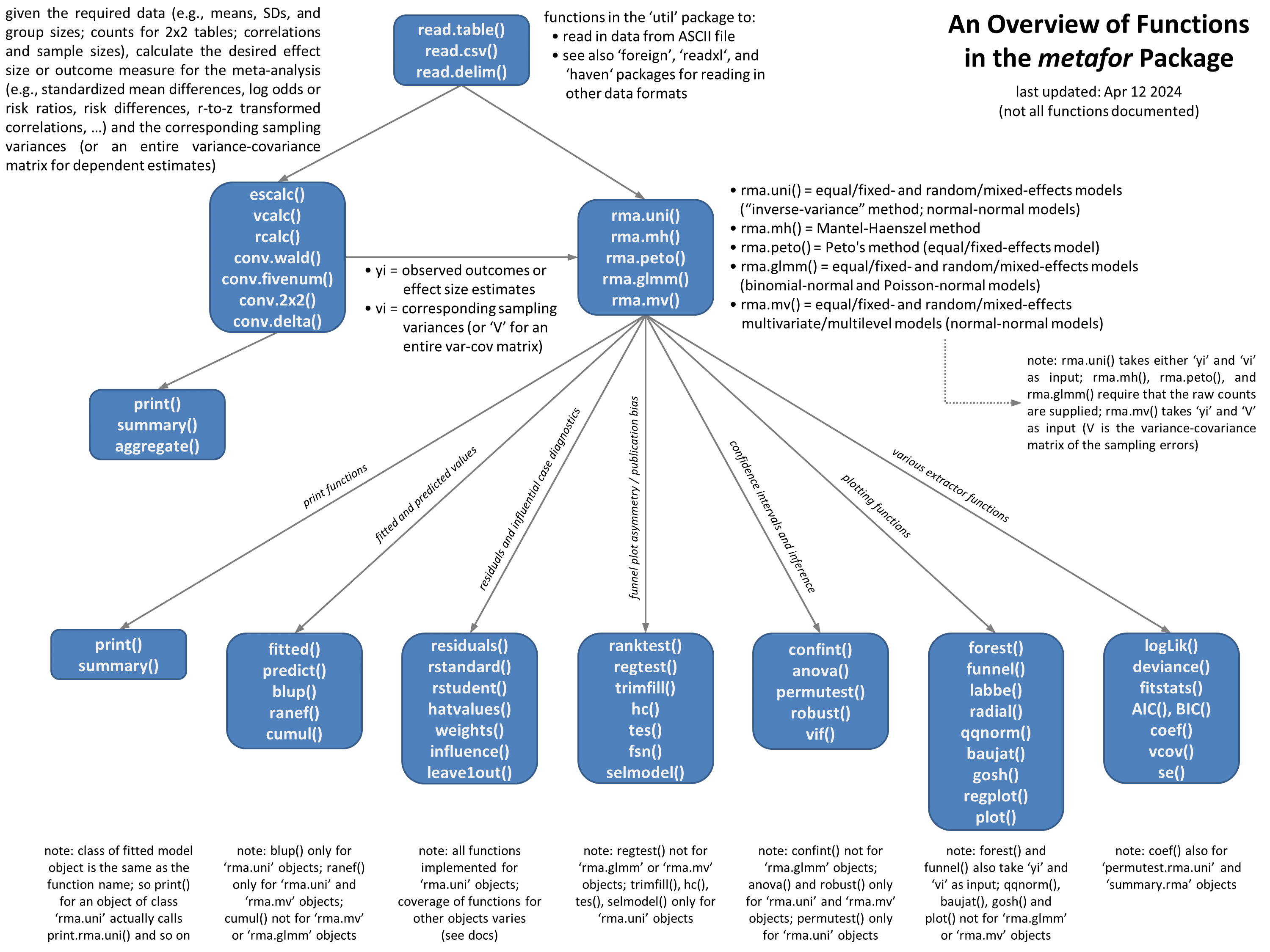
Overview of the functions of metafor (from the official website of metafor-project)
Secondly, the analytical strategy can be adjusted according to the purpose and aims of the research.
Take-away messages
- As a meta-analysis technique that uses the reliability coefficient
as the effect size, reliability generalization has both the common and
specificity of meta-analysis.
- Find out if there is a “Reliability Induction” issue.
- Comprehensively evaluate whether a tool is stable and reliable.
metaforprovides more options for the implementation of statistical analysis of reliabilit generalization.- Choose the appropriate analysis method according to the aim.
4. Resources
4.1 CRAN documentation
Since the developer will update the R package, the code need to be used based on the manual if any updates.
help(metafor) #manual
? metaphor## No documentation for 'metaphor' in specified packages and libraries:
## you could try '??metaphor'? escalc()
#escalc# Take escalc() as an example to look at the source code to understand the underlying logic4.2 metaforofficial website
Here are two useful websites that provide a lot of resources.
metafor@github
[Metafor-Project website] (https://www.metafor-project.org/doku.php).
4.3 Reference books
Harrer, M., Cuijpers, P., Furukawa, T. A., & Ebert, D. D. (2021). Doing meta-analysis with R: A hands-on guide. Chapman and Hall/CRC.
Polanin, J. R., Hennessy, E. A., & Tanner-Smith, E. E. (2017). A Review of Meta-Analysis Packages in R. Journal of Educational and Behavioral Statistics, 42, 206–242.
Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36, 1–48.